SCC와 2-SAT

SCC

SCC는 Strongly Connected Component의 약자로, 방향 그래프의 SCC는 다음 조건을 만족하는 서브그래프들입니다.

같은 SCC 내에 속하는 임의의 서로 다른 두 정점은 서로 도달 가능합니다.
어떤 정점이나 간선도 1의 조건을 만족하면서 이 SCC에 추가될 수 없습니다.(최대부분집합)

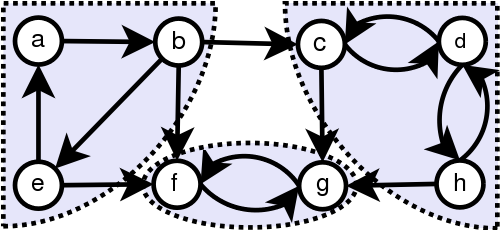
SCC Example

위의 예시에서는 (a, b, e) (f, g) (c, d, h)가 하나의 SCC가 됩니다. 임의의 방향 그래프에서 SCC를 구했을 때 모든 정점은 단 하나의 SCC에만 속하게 되며, SCC 자체를 하나의 정점으로 보았을 때 전체 그래프를 사이클이 없는 방향 그래프(DAG) 형태로 변환할 수 있습니다.

임의의 방향 그래프가 주어질 때 SCC를 찾는 알고리즘으로 코사라주의 알고리즘과 타잔의 알고리즘이 유명하고, 둘 모두 $O(V+E)$ 에 동작함이 증명되어 있습니다. 아래는 각 알고리즘의 설명과 구현 코드입니다. 입출력은 BOJ의 Strongly Connected Component 문제를 기준으로 작성했습니다.

코사라주의 알고리즘(Kosaraju’s Algorithm)

코사라주의 알고리즘은 다음과 같이 동작합니다.

방향 그래프 G, 빈 스택 S, G의 간선 방향을 뒤집은 역방향 그래프 G’를 준비합니다.
G에서 아직 방문되지 않은 정점들에 대해 DFS를 시행하고, 각 정점의 탐색이 끝나는 순서대로 S에 넣습니다.(위상정렬) 스택에 모든 정점이 들어갈 때까지 반복합니다.
S가 빌 때까지 다음을 반복합니다.
S의 가장 위쪽에 있는 정점 v를 뽑습니다. v가 G’에서 이미 방문된 정점이라면 정점을 다시 뽑습니다.
G’에서 v에서 DFS를 시행해 이번 시도에 처음 방문한 정점들을 v와 같은 SCC로 묶습니다.

코사라주의 알고리즘은 정방향 그래프와 역방향 그래프가 동일한 SCC를 가진다는 점을 이용합니다. 정방향 DFS를 통해 정점들을 위상정렬하고, 역방향 DFS에서 SCC를 찾는다고 생각할 수 있습니다.

Kosaraju's Algorithm Code

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;
const int MAX = 10020;

int V, E;
vector < int > front[MAX], rev[MAX];

void input() {
    scanf("%d%d", &V, &E);

    // 그래프 초기화
    for (int i = 0; i < E; i++) {
        int f, s;
        scanf("%d%d", &f, &s);
        front[f].push_back(s);
        rev[s].push_back(f);
    }
}

int visited[MAX], stack[MAX], top;
vector < vector < int > > sccGroup;

void front_dfs(int node) {
    visited[node] = 1;
    for (auto next : front[node]) {
        if (!visited[next]) {
            front_dfs(next);
        }
    }
    // DFS를 빠져 나올 때 스택에 쌓음
    stack[top++] = node;
}

void rev_dfs(int node) {
    visited[node] = 1;
    // 마지막 그룹에 정점 추가
    sccGroup[sccGroup.size()-1].push_back(node);
    for (auto next : rev[node]) {
        if (!visited[next]) {
            rev_dfs(next);
        }
    }
}

void solve() {
    // 위상 정렬
    for (int v = 1; v <= V; v++) {
        if (!visited[v]) {
            front_dfs(v);
        }
    }

    // 그룹 묶기
    memset(visited, 0, sizeof(visited));
    while (top) {
        int node = stack[top-1];
        top--;
        if (!visited[node]) {
            // 빈 그룹 추가
            sccGroup.push_back(vector < int >());
            rev_dfs(node);
        }
    }

    // 문제 요구 조건대로 정렬
    for (auto &vec : sccGroup)
        sort(vec.begin(), vec.end());
    sort(sccGroup.begin(), sccGroup.end());

    // 출력
    printf("%dn", sccGroup.size());
    for (auto &vec : sccGroup) {
        for (auto elem : vec) {
            printf("%d ", elem);
        }
        puts("-1");
    }
}

int main() {
    input();

    solve();

    return 0;
}

코사라주의 알고리즘은 기억하기 쉬운 편이지만, 동일한 그래프를 두 가지 형태로 저장해야 하고 DFS를 두 번 시행하기 때문에 일반적으로 타잔의 알고리즘보다 약간 낮은 성능을 보여줍니다. 하지만 시간복잡도에는 차이가 없기 때문에 알고리즘 문제풀이에서는 문제 없이 사용할 수 있습니다.

타잔의 알고리즘(Tarjan’s Algorithm)

타잔의 알고리즘은 다음과 같이 동작합니다.

방향 그래프 G, 빈 스택 S, 각 정점의 방문 순서를 저장할 배열 index, 각 정점에서 도달 가능한 정점을 저장할 배열 lowlink를 준비합니다.
아직 방문되지 않은 정점 v에서 DFS를 시작합니다.
v를 S에 쌓고, index[v]에 방문 순서를 저장합니다.
lowlink[v] = index[v]
v의 이웃 정점 u에 대해:
u를 아직 방문하지 않았다면 u에 대해 DFS를 시행하고, lowlink[u]가 lowlink[v]보다 작은 경우 lowlink[v]를 갱신합니다.
u가 스택에 들어있고, index[u]가 lowlink[v]보다 작은 경우 lowlink[v]를 갱신합니다.
lowlink[v]와 index[v]가 동일하다면, v를 포함해 v 이후로 S에 쌓인 정점들을 새로운 SCC 컴포넌트로 묶습니다.

타잔의 알고리즘은 각각의 SCC가 DFS 트리에서 서브트리를 이룬다는 점을 이용한 알고리즘입니다. 임의의 정점 v에 대한 탐색이 종료된 시점에서, v 이전에 스택에 쌓인 정점에 대한 경로가 존재하는 경우에만 v가 스택에 남아 있을 수 있습니다. 그렇지 않은 경우 v는 v 이전에 스택에 쌓인 정점들과 같은 SCC에 속할 수 없기 때문에 v가 SCC의 경계가 되어 현재 스택에 쌓인 정점들과 SCC를 구성합니다.

Tarjan's Algorithm Code

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;
const int MAX = 10020;

int V, E;
vector < int > from[MAX];

void input() {
    scanf("%d%d", &V, &E);

    // 그래프 초기화
    for (int i = 0; i < E; i++) {
        int f, s;
        scanf("%d%d", &f, &s);
        from[f].push_back(s);
    }
}

int stack[MAX], top, id[MAX], currentId, groupId[MAX];
vector < vector < int > > sccGroup;

int traverse(int node) {
    id[node] = ++currentId;
    stack[top++] = node;

    // lowlink를 return 값으로 사용
    int lowlink = id[node];
    for (auto next : from[node]) {
        if (id[next] == 0) {
            // 방문하지 않은 정점
            lowlink = min(lowlink, traverse(next));
        } else if (groupId[next] == 0) {
            // 이미 스택에 들어 있는 정점
            lowlink = min(lowlink, id[next]);
        }
    }

    if (lowlink == id[node]) {
        // 그룹 추가
        sccGroup.push_back(vector < int >());
        while (1) {
            int now = stack[top-1];
            top--;

            // node 하위의 서브트리를 SCC 그룹으로 묶기
            groupId[now] = sccGroup.size();
            sccGroup[groupId[now]-1].push_back(now);

            if (now == node) break;
        }
    }

    return lowlink;
}

void solve() {
    for (int v = 1; v <= V; v++) {
        if (id[v] == 0) {
            traverse(v);
        }
    }

    // 문제 요구 조건대로 정렬
    for (auto &vec : sccGroup)
        sort(vec.begin(), vec.end());
    sort(sccGroup.begin(), sccGroup.end());

    // 출력
    printf("%dn", sccGroup.size());
    for (auto &vec : sccGroup) {
        for (auto elem : vec) {
            printf("%d ", elem);
        }
        puts("-1");
    }
}

int main() {
    input();

    solve();

    return 0;
}

타잔의 알고리즘은 기억해야 할 조건들이 코사라주의 알고리즘에 비해 헷갈리는 편이지만, DFS를 한 번만 작성해도 된다는 점에서 타잔의 알고리즘을 더 쉽다고 평가하는 의견도 있습니다. 둘 모두 시간복잡도는 동일하기 때문에 문제를 풀 때는 일반적으로 어떤 알고리즘을 사용해도 괜찮습니다.

2-SAT

SCC 알고리즘의 응용 사례 중 유명한 것으로 2-SAT 문제가 있습니다. SAT 문제는 논리 변수와 논리식이 주어질 때 논리식을 참으로 만드는 논리 변수 조합이 존재하는지를 찾는 문제입니다. 2-SAT은 SAT 문제들 중 특수한 형태의 문제로, 다음 예시에서 볼 수 있듯이 두 개의 변수의 or 연산들이 and 연산으로 결합된 형태의 논리식을 다루는 문제입니다. 이런 형태의 식을 2-CNF 또는 Krom formulas라고 부릅니다.

$(neg x_1 vee x_3) wedge (neg x_2 vee neg x_3) wedge (x_1 vee x_2) wedge (neg x_1 vee x_4) wedge (x_2 vee neg x_4)$

이제 논리식을 그래프로 바꾸는 방법을 알아봅시다.

각각의 논리 변수 $x$ 에 대해 두 개의 정점 $x, ~neg x$ 을 생성합니다.
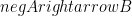논리식에 포함된 각각의 $A vee B$ 에 대해, $neg A rightarrow B$ 간선과 $neg B rightarrow A$ 간선을 생성합니다.

위의 예시에서 보여드린 식을 그래프로 바꾸면 다음과 같습니다.

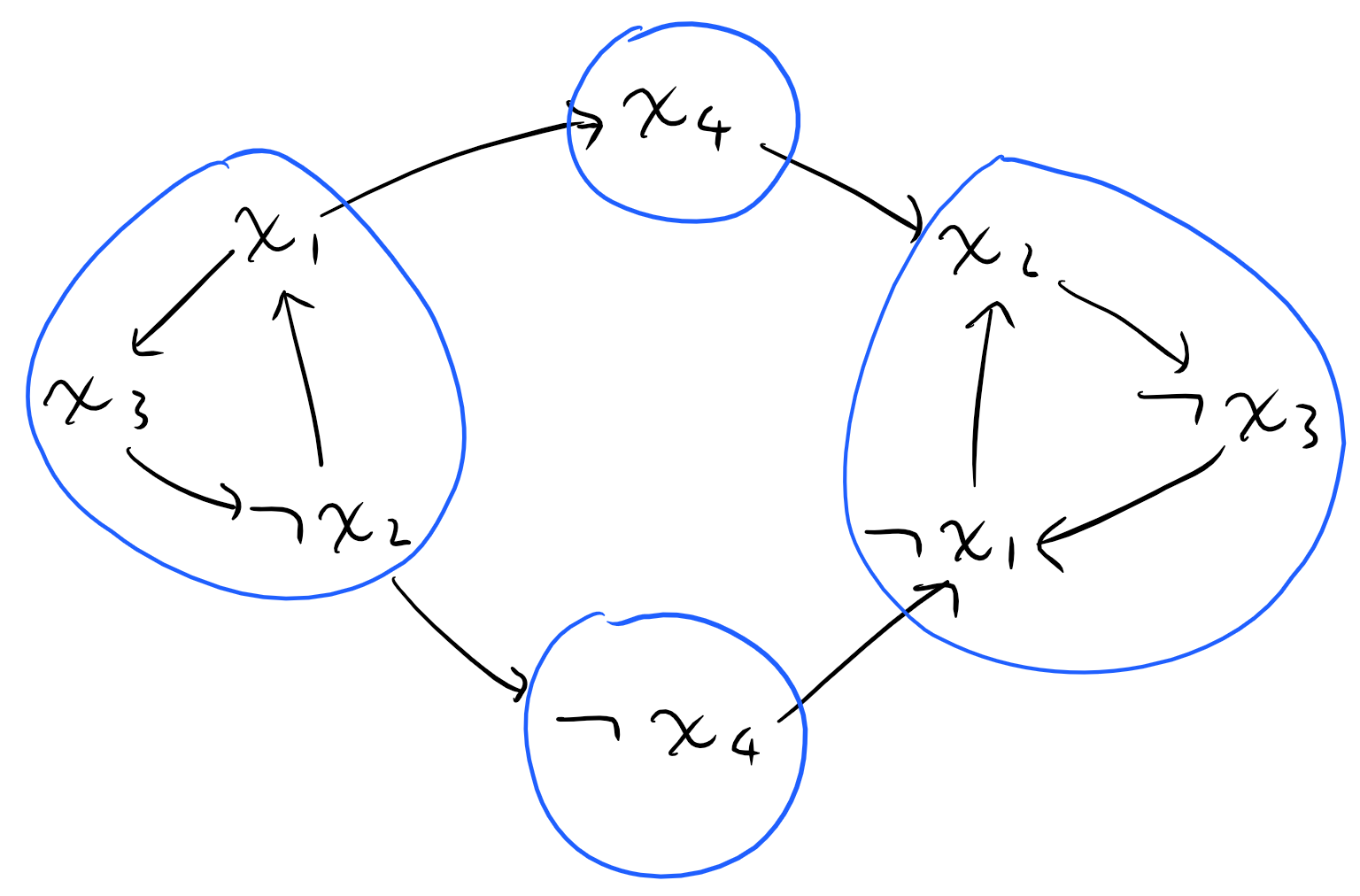
이렇게 그래프를 생성하면 or로 묶인 두 개의 변수 중 적어도 하나는 참이어야 하기 때문에, A에서 B로 가는 간선은 A가 참이라면 B도 반드시 참이라는 것을 의미하게 됩니다. 이제 이 그래프에 SCC 알고리즘을 적용해서 정점들을 컴포넌트로 묶은 이후를 생각해봅시다. SCC의 정의와 간선을 그은 조건 때문에, 컴포넌트 내에 하나의 정점이라도 참이라면 그 컴포넌트는 모두 참이 됩니다. 따라서 같은 컴포넌트에 속한 정점들은 전부 참이거나 전부 거짓이라는 것을 알 수 있습니다.

$x$ 와 $neg x$ 는 다음 세 가지 중 한 가지 관계를 가집니다.

$x$ 와 $neg x$ 가 같은 컴포넌트에 속하는 경우
$x$ 에서 $neg x$ 로 가는 경로(또는 $neg x$ 에서 $x$ 로 가는 경로)만 존재하는 경우
$x$ 와 $neg x$ 간에 경로가 존재하지 않는 경우

첫 번째는 답이 존재하지 않는 경우입니다. 주어진 논리식을 참으로 만드는 논리 변수 조합이 존재하는 것과, 논리 변수 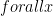$forall x$ 에 대해 $x$ 와 $neg x$ 정점이 같은 컴포넌트에 속하지 않는 것이 필요충분조건임이 증명되어 있습니다.

두 번째는 위상정렬 했을 때 더 뒤쪽에 존재하는 정점만이 참입니다. 세 번째는 둘 중 어느 것을 참으로 결정해도 상관 없습니다.

그래프가 skew-symmetric하기 때문에 $A, ~B$ 가 같은 컴포넌트에 속한다면 $neg A, ~neg B$ 또한 같은 컴포넌트에 속하고, 이 특징을 이용해 위의 성질들을 증명할 수 있습니다.

위의 성질들을 이용해 각 논리 변수의 값을 다음 방법으로 찾을 수 있습니다.

논리식에서 그래프를 생성합니다.
생성된 그래프에 SCC 알고리즘을 적용합니다.
만약 $x$ 와 $neg x$ 의 SCC 번호가 같은 정점이 존재한다면 주어진 논리식을 만족하는 조합은 존재하지 않습니다.
아니라면, $x$ 의 SCC 번호가 $neg x$ 의 SCC 번호보다 작은 경우 $x$ 가 참입니다.

아래는 구현 코드입니다. BOJ의 2-SAT – 4 문제를 기준으로 작성했습니다.

2-SAT

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;
const int MAX = 20020;

int N, M;
vector < int > from[MAX];

inline int neg(int x) {
    if (x > N) return x - N;
    else return x + N;
}

void input() {
    scanf("%d%d", &N, &M);

    // 그래프 초기화
    for (int i = 0; i < M; i++) {
        int f, s;
        scanf("%d%d", &f, &s);

        // ~X는 N+X로 표현
        if (f < 0) f = -f + N;
        if (s < 0) s = -s + N;

        from[neg(f)].push_back(s);
        from[neg(s)].push_back(f);
    }
}

int stack[MAX], top, id[MAX], currentId, groupId[MAX];
vector < vector < int > > sccGroup;

int traverse(int node) {
    id[node] = ++currentId;
    stack[top++] = node;

    // lowlink를 return 값으로 사용
    int lowlink = id[node];
    for (auto next : from[node]) {
        if (id[next] == 0) {
            // 방문하지 않은 정점
            lowlink = min(lowlink, traverse(next));
        } else if (groupId[next] == 0) {
            // 이미 스택에 들어 있는 정점
            lowlink = min(lowlink, id[next]);
        }
    }

    if (lowlink == id[node]) {
        // 그룹 추가
        sccGroup.push_back(vector < int >());
        while (1) {
            int now = stack[top-1];
            top--;

            // node 하위의 서브트리를 SCC 그룹으로 묶기
            groupId[now] = sccGroup.size();
            sccGroup[groupId[now]-1].push_back(now);

            if (now == node) break;
        }
    }

    return lowlink;
}

void solve() {
    for (int v = 1; v <= 2*N; v++) {
        if (id[v] == 0) {
            traverse(v);
        }
    }

    // x와 ~x가 같은 컴포넌트 안에 속하면 답 없음
    for (int v = 1; v <= N; v++) {
        if (groupId[v] == groupId[neg(v)]) {
            puts("0");
            return;
        }
    }

    // x가 ~x보다 컴포넌트 번호가 작은 경우(그래프 상에서 뒤에 있는 경우) x는 참
    puts("1");
    for (int v = 1; v <= N; v++) {
        printf("%d ", groupId[v] < groupId[neg(v)]);
    }
    puts("");
}

int main() {
    input();

    solve();

    return 0;
}

6 댓글

Junho Han 댓글:

2016년 9월 20일, 11:19 오후

2-SAT 마지막 줄에
“4. 아니라면, x의 SCC 번호가 \neg x의 SCC 번호보다 작은 경우 x가 참입니다.”
이부분 타잔알고리즘 썼을 때만 적용되는 것 같아요! 코사라주와 타잔이 scc번호 매기는 순서가 반대라서 코사라주일 때는 반대여야 할 것 같습니다!

응답
Junho Han 댓글:

2016년 9월 20일, 11:26 오후

글 잘보고 가요~ 설명 짱짱

응답
DongSeong Go 댓글:

2016년 9월 28일, 8:09 오후

하… 정말 설명 잘해놓으셨네요 힐링됩니다.. 감사합니다

응답
익명 댓글:

2017년 5월 23일, 8:01 오후

감사합니다…

응답
LukeKim 댓글:

2017년 6월 6일, 1:02 오후

와우 잘보고가요 감사합니다!!!

응답
Beomjin Ahn 댓글:

2018년 7월 15일, 1:07 오후

덕분에 투셋 알고리즘 배워갑니다!!

응답