몇 달동안 계속 풀려고 시도 중인 JOI 전압을 코딩 도전해 보고 있는데, 오랜만에 문제 푸는 김에 코딩 습관도 바꿔 보려고 한다.

1

일단 자바스크립트랑 액션스크립트를 하면서 생긴 버릇인데, 얘들은 블록 스코프가 없어서 for문 인덱스 변수를 바깥에 선언해 주어야 한다.

var i;
for (i = 0; i < n; i++);

그런데 블록 스코프가 있는 언어 다른 언어에서 이렇게 쓰면 코드가 길어지고 큰 이득이 없는 것 같아서 일단 for문 내부 스코프 사용하는 for (int i = 0; i < n; i++) 방식으로 변경해 보려고 한다. 이렇게 쓸 때 문제는 for문 안에서 break하고 다 돌았는지 아닌지 i랑 n이랑 비교하면서 검사할 때 비교가 불편하다는게 있긴 한데 일단은 시험삼아 적용해 보는 것으로 결정.

2

1이랑 연관된 내용. for문 인덱스 변수로 보통 ijk를 많이 사용해 왔는데 되도록이면 의미있는 이름을 짓기로 했다.

이건 예전부터 생각해왔던 건데 타이밍이 애매해서 못 바꾸고 있었다. 몇 주 코딩 쉬다가 다시 복귀하는 타이밍이 괜찮아서 이 참에 이 습관도 바꾸기로 함.

구글 코드잼 2015가 끝났다. R2 치고 나서 결과를 안 올렸었는데 R3랑 같이 최종 결산하면서 한꺼번에 올리기로 했다.

R2

A

A는 격자 밖으로 나가는 발판들을 전부 센 뒤, 조건대로 처리할 수 없는 발판이 있는지를 확인하는 단순한 탐색 문제였다.

16:33 AC

D

A를 풀고 나서, B와 C를 읽기는 했다. 둘 다 조금씩 끄적여 봤지만 전혀 풀이가 떠오르지 않았고, D는 풀이는 잘 떠오르지 않았지만 문제가 내 취향이고 배점도 높아서 D를 풀기로 했다. D는 가로 시작과 끝이 이어지는 원통 형태의 평면에서 각 칸에 숫자를 써 상하좌우 인접한 칸에 그 숫자가 딱 그 개수만큼 있도록 만들 수 있는 가짓수를 세는 문제였다.(2를 썼다면 상하좌우에 2가 두 개 있어야 함)

바로 감이 오는 건 없었지만 작은 숫자에 대해 백트래킹을 구해 규칙성을 관찰했고, 포함배제를 이용해 패턴을 겹치지 않게 잘 세어주면 된다. 빠트린 패턴이 있어서 두 번 WA를 받았다.

2:26:27 AC

결산

B는 각 수도꼭지의 온도와 단위 시간당 물의 양이 주어질 때, 원하는 만큼의 물을 원하는 온도로 맞추기 위해 필요한 최소 시간을 묻는 문제였다. 2차원 벡터를 합해 원하는 벡터를 만드는 형태의 문제로 변환해서 풀 수 있다고 한다. C는 두 개의 언어 사이에 공통되도록 사용되는 단어를 세는 문제였는데 Flow 문제라고 한다. 둘 다 풀이를 듣고 나니 내가 잘 못 푸는 유형이 맞았다. 대회 끝나고 나서 연습하긴 할텐데 대회 때 넘긴 건 잘한 선택이었다고 생각한다.

304위로 마무리했고 티셔츠와 함께 R3 진출권을 얻었다.

R3

B

A 풀이를 깊게 생각하지 않고 이렇게 짜면 되려나 싶어서 짰는데, 완전히 잘못된 방향의 접근이었다는 것을 거의 다 짰을 때쯤 되서 깨달았다. 일단은 지금 고치기에는 너무 멀리 왔다고 판단되어 A를 넘기고 B부터 풀었다. B는 문제 읽고 나서 바로 그리디 알고리즘을 떠올렸고, 코드도 금방 짤 수 있었다.

두 번 WA를 받았는데 한 번은 음수 modular가 음수가 나온다는 사실 때문이었고 다른 한 번은 offset 계산을 하지 않아서였다. 두 문제를 고치고 나서 맞을 수 있었다.

1:23:42 AC

A

B를 풀고 나서 다시 A를 잡았다. 새로 떠올린 A 풀이는 정확히 증명하진 않았지만 Sliding Window 기법으로 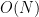이라고 생각한 풀이를 짰다. 초기화 부분에서 빠트린 게 있어서 찾느라 한참 걸렸고, 대회 마감 1분 30초 정도를 앞두고 틀린 부분을 찾을 수 있었다. 데이터를 넣고 돌리는데 이상하게 오래 걸리는 느낌이 들었지만 다행히 시간 내에 답이 다 나왔다. 대회 끝나고 나서 다시 생각해보니 최악의 경우 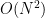이 걸리는 풀이였다. 문제에서 데이터를 직접 입력하지 않고 선형합동생성기로 생성하기 때문에 문제 없이 돌아갔던 것 같다.

2:29:40 AC

결산

끝나기 직전에 겨우 A, B를 풀었기 때문에 등수가 높지 않을 것으로 예상했는데 163위라는 생각보다 높은 등수로 마무리했다. C, E는 읽어보지 못했고 D는 읽어봤는데 시간을 주면 풀 수 있을 것 같은 문제라고 느꼈다. A를 풀고 나서 대회가 바로 종료되었기 때문에 건드려 볼 시간이 없었다. 예상대로 onsite는 진출하지 못했지만(전세계에서 25명 뽑는다) 생각보다 좋은 결과를 얻었다고 생각한다.

종합 후기

이번 대회에서 가장 보람찼던 건 ‘말리지 않았다’는 점이다. 고등학교 때부터 대회만 있었다 하면 자꾸 사소한 실수를 못 찾고 계속 붙잡고 있다가 망하는 경우가 많았다. 특히 대회가 중요하면 중요할수록 심리적 압박감 때문에 이런 현상이 심해졌다. KOI도 세 번 은상만 받고 끝났고, 계절학교 때는 그렇게 잘 하다가도 선발고사만 보면 매 번 기대 이하의 성적을 거두곤 했다. 하지만 이번 코드잼에서는 실수가 있더라도 긴장하지 않고 차근차근 찾아내 결국 다 해결할 수 있었다. 내 실력이면 이 정도는 풀어야 한다고 느꼈던 문제들은 다 풀었고, 시간을 더 주면 풀 수 있을 것 같은데 못 풀었던 문제들이 좀 있었다. R3까지 와 보는 건 처음인데 느리지만 꾸준히 성장하고 있다는 것을 느낄 수 있었고, 앞으로도 성장할 여지가 많이 남아 있다는 것을 느낀 의미 있는 대회였다.

대시보드

결과부터 말하자면 B Large를 제외한 모든 문제를 해결했고, 133위로 순조롭게 Round 2에 진출했다. R1A는 시험을 쳤지만 1000등 밖이라 떨어졌고, R1B도 칠 예정이었는데 과 MT랑 날짜가 겹쳐서 가서 어떻게든 쳐보려고 노트북을 들고 갔지만 인터넷이 안 되서 결국 R1C에서 통과하게 되었다.

A

A는 Battleship이라는 게임에서 파생된 간단한 게임 문제로, 두 사람이 최적의 해로 플레이할 때 게임이 얼마나 오래 지속되는지를 묻는 문제였다. small은 1차원, large는 2차원상에서 문제를 해결해야 하지만 배의 방향이 고정되어 있어 풀이가 크게 달라지지는 않는다. 한 번 위치를 부를 때 배가 있을 수 있는 가능성이 W개 줄어든다는 것을 관찰하면 쉽게 탐욕 알고리즘을 세울 수 있다.

28:37 AC

B

무한한 수의 원숭이들에게 타자기를 하나씩 쥐어 주고 무한한 시간이 흐르면 그 중 한 마리는 셰익스피어의 햄릿을 완성시킬 것이다.

B는 위의 유명한 농담에서 파생된 문제다. 목표 문장과 원숭이의 타자기가 주어지고, 원숭이가 몇 글자를 누르는지가 주어지면 원숭이가 목표 문장을 완성하는 횟수의 기대값을 구하는 문제였다. 일단 풀이는 생각이 났지만 동적 계획법과 문자열 매칭 알고리즘을 응용하는 지나치게 복잡한 풀이라 우선은 전부 만들어보는 naive한 방법으로 small만 해결했다.

38:56 AC

C

C는 화폐 개혁을 통해 사용 가능한 동전 개수를 최소로 추가하면서 특정 금액을 지불할 수 있도록 만드는 문제였다. 보자마자 떠올린 알고리즘이 맞았고, 목표 금액이 아주 큰 경우에서 실수한 것 때문에 한 번 WA를 받고 통과했다.

54:16 AC

전체 후기

문제를 풀면서 예상했던대로 B Large는 훨씬 쉬운 풀이가 존재했다. 나는 한 번 길을 잘못 들면 잘못된 풀이에 계속 빠져 있는데, 그걸 잘 파악해서 B Large를 빠르게 넘기고 C를 푼 게 이번 라운드의 성공 요인이라 생각한다. 100점이 아닌 사람들 중에서는 1위를 했고, 라운드 초반에는 잠깐이나마 Top 10에도 올라갔었기 때문에 성공적이었다고 생각한다.

이번에 못 풀었던 B Large 복습하고 R2에서도 좋은 결과를 얻어 올해는 꼭 티셔츠를 받고 싶다!

풀이 스포 주의. 일단 결과부터 말하자면 1047위로 아슬아슬하게 떨어졌다. R1B랑 R1C가 있으니 문제는 없지만 작년 정올 이후로 거의 문제를 안 풀었더니 실력이 줄어든것 같아 슬프다.

A

A에서 시간 낭비를 많이 한 게 탈락의 가장 큰 원인이라고 생각된다. 문제 이해를 잘못해서 2번 케이스에서 rate가 정수여야 한다고 멋대로 가정하고 풀면서 왜 예제 마지막 케이스가 244인지를 이해하지 못하고 있었다. 5분컷 가능한 문제인데 30분만에 AC.

B

풀이는 금방 찾았는데 코드에서 B랑 N을 헷갈리는 바람에 이것도 시간을 쓸 데 없이 썼다. 풀이 자체는 time으로 파라메트릭 돌리는 전형적인 문제.

C

처음에 접근한 방법은 컨벡스헐 구하고 컨벡스헐 위의 두 점을 으로 잡고 적절히 영역을 잘 잡아서 영역안의 점들을 하나씩 제거하면서 처리하면 에 되지 않을까 했는데 이렇게 저렇게 바꿔봐도 안 되길래 포기.

두 번째는 왠지 컨벡스헐 구한 다음 한 껍질을 벗기면 다음 컨벡스헐에 포함된 점들의 값은 1이고 그 다음은 2고 이런식으로 나아갈 것이라고 멋대로 추측하고 열심히 짰으나 예제부터 안 나옴. 짜기 전에 잘 볼 걸… 짜서 돌려보고 나니까 왜 이게 답일 것이라 추측했는지 모르겠다.

시간이 얼마 안 남았길래 틀린 코드들을 짜면서 중요한 부분은 다 짰으니 급하게 지수 알고리즘으로 C Small이라도 풀어서 내려고 했으나 WA. 아직 어디를 틀렸는지 못 찾았는데 이것도 B처럼 멍청한 실수를 했을듯한 기분이 든다.

C Large가 풀면서 실력 쌓기 좋은 문제라고 판단되어 대회 끝나고 생각하는 중이었는데 그 직후 트위터에 Bumsoo Park가 올린 C 풀이를 보고 말았다. 다행히 내 의식의 흐름 속에 있었던 풀이라 많이 안타깝지는 않았다. 가장 처음 접근했던 방법을 convexhull-wise에서 point-wise로 바꿔서 처리하면 된다고 한다.

C 코드 저장해 뒀다가 틀린 부분 찾고, 나중에 C Large 짜 보는 것으로 하고 R1A는 여기서 마무리.